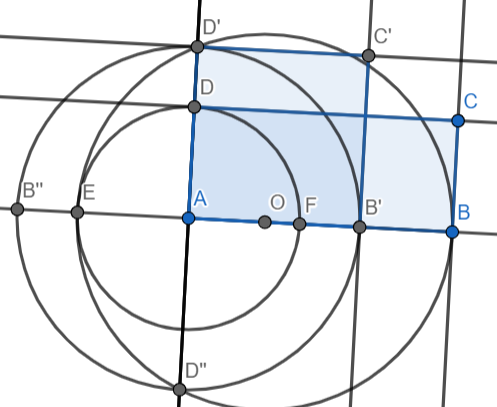
Soit \(A,B,C,D\) les quatre sommets d'un rectangle donné
Construire les quatre sommets du carré \(AB^\prime C^\prime D^\prime\) de même aire que \(ABCD\) et tels que \(B^\prime\in[AB)\) et \(D^\prime\in[AD)\)

"ramener" \(D\) sur la droite \((AB)\)
$$\mathcal C(A,D)\cap(AB)=\{E,F\}\quad\text{ avec }\quad F\in[A,B)$$

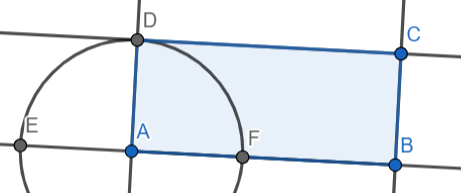
Tracer un cercle utile pour la puissance
On veut \(\underbrace{AE\cdot AB}_{{\text{rectangle}}}=\underbrace{AD^{\prime2}}_{\text{carré}}\) (car on veut les aires égales)
Soit \(O=\frac{E+B}2\) et \(\mathcal C=\mathcal C(O,E)\)

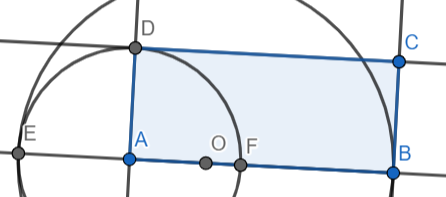
Nommer les points intéressants et utiliser la formule de la puissance
On a alors : $$AE\cdot AB=-P_\mathcal C(A)=AD^\prime\cdot AD^{\prime\prime}=AD^{\prime2}\quad\text{ car }\; AD^{\prime\prime}=AD^\prime$$

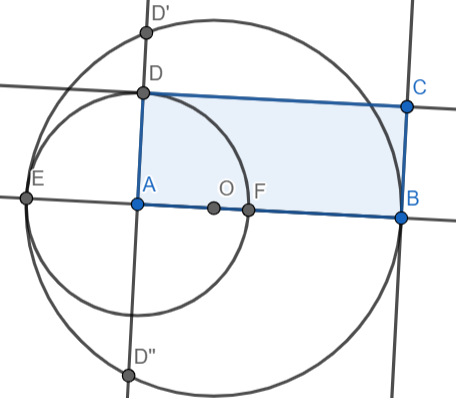
En déduire la position de \(B^\prime\) via un cercle (qui conserve les distances)
$$\mathcal C(A,D^\prime)\cap(AB)=\{B^\prime,B^{\prime\prime}\}\quad\text{ avec }\quad B^\prime\in[AB)$$

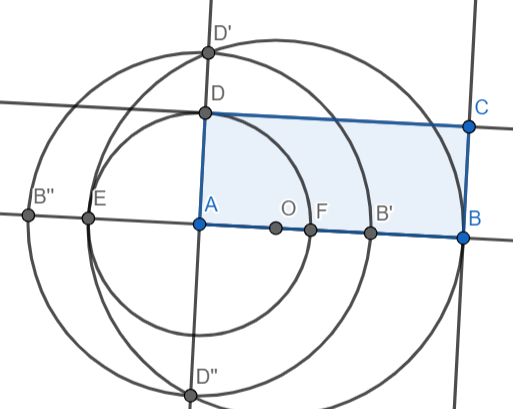
En déduire la position de \(C^\prime\) (dernier point du carré)

La perpendiculaire à \((AB)\) passant par \(B^\prime\) et la perpendiculaire à \((AD)\) passant par \(D^\prime\) se coupent en \(C^\prime\)